【论文阅读笔记】Contrastive Attributed Network Anomaly Detection with Data Augmentation
Title:Contrastive Attributed Network Anomaly Detection with Data Augmentation
Source: PAKDD CCF-C
动机:
whether the prior human knowledge of different anomaly types could be harnessed to advance anomaly detection on attributed networks.
即:希望把关于异常类型的先验知识用到异常检测工作上
仍有两个挑战:
- 挑战 1:知识建模,如何恰当的对先验知识进行建模。现有方法通常是将这部分知识作为原始 input 之外的输入
- 挑战 2:知识整合,如何将先验知识集成到模型中,常见的是将它们变成显式的监督信号,并且设计 loss 集成到模型中,作者认为不应只是通过损失函数,而是要有灵活的集成方式
于是本文提出 CONAD(Contrastive Anomaly Detection)——“A principled contrastive anomaly detection framework”,有如下改进或创新:
- 为了解决知识建模的挑战,提出了数据增强策略,将不同的异常类型建模成对比样本
- 解决知识整合挑战,采用 Siamese GNN(孪生 GNN),用一个 encoder 将属性网络和增广属性网络映射到一个新的嵌入空间,用对比损失 + 重构损失联合进行优化,端到端训练。检测阶段用重构误差来衡量
问题定义
(本文的研究对象是属性网络)
\mathcal{G} = \{\mathbf{A}, \mathbf{X} \},邻接矩阵和属性,异常检测任务则是给每个节点 assign 一个异常分数;带上先验知识 \xi(结合进具体的数据中表示为 \text{M}(\xi))后的 \mathcal{G} 就是本文追求的方法
方法-CONAD
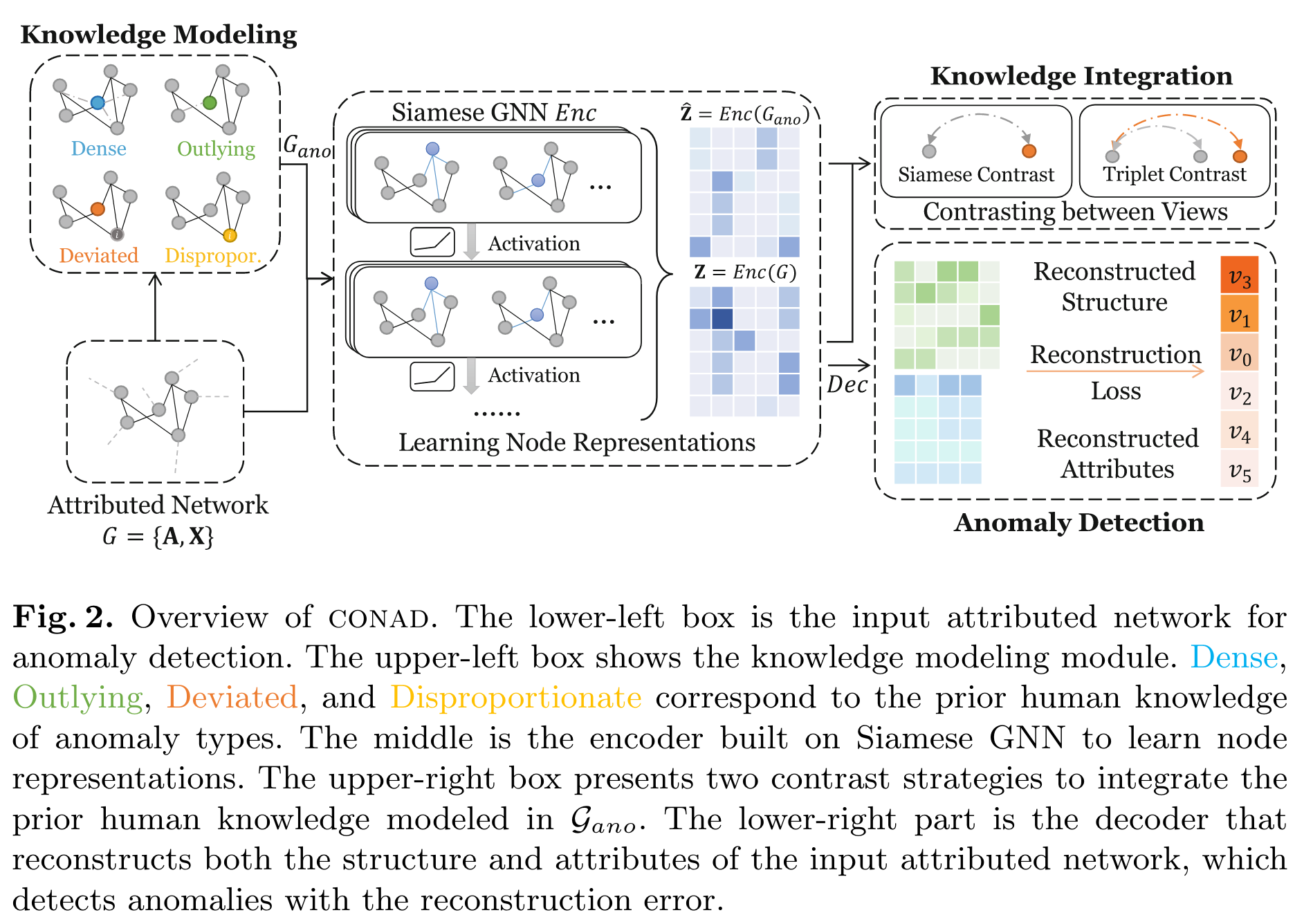
架构解释: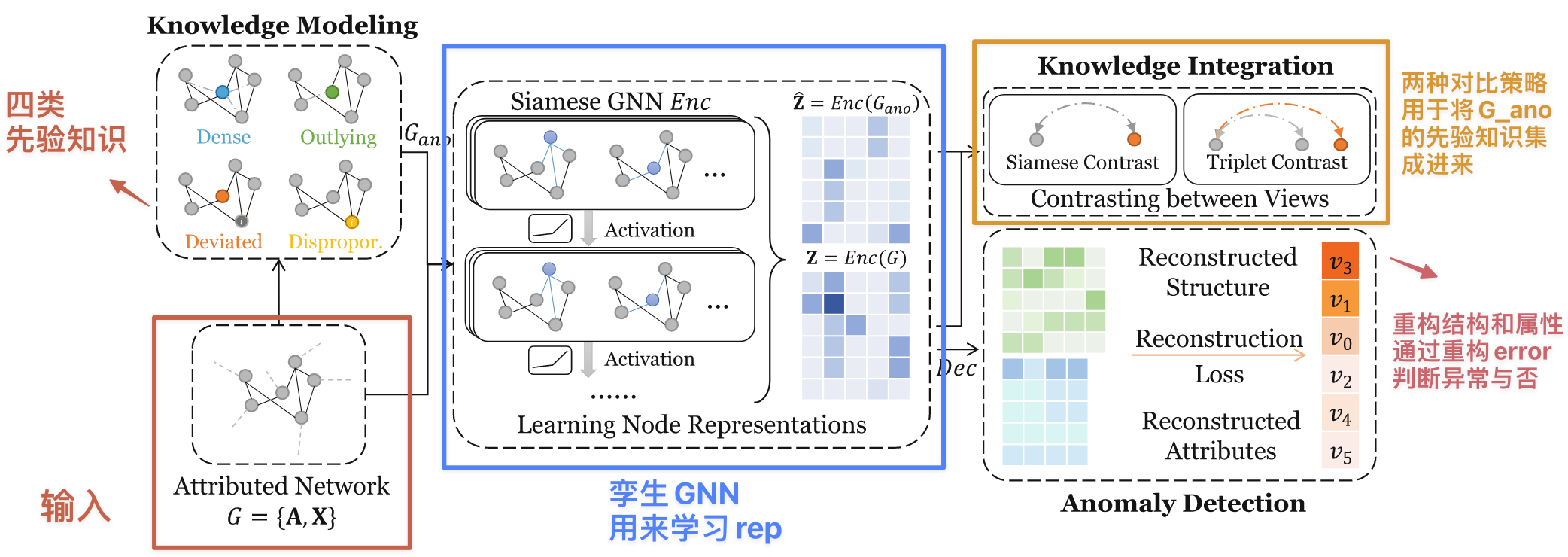
知识建模 module(感觉其实就是类似别人的异常注入的那一步)
分成四类,两个 structure,两个 attribute 的异常先验知识:
- 结构,high-degree:从具有平均度的节点中选择一些然后把他们随机给其他的节点连接上
- 结构,outlying:随机丢弃掉某个节点的大部分边,使它看起来不属于任何社区
- 属性,deviated:属性值偏离其邻居的节点。先选择一些中心节点,然后从整个网络中随机抽样一些节点,计算相似度,然后把相似度最小的节点的属性给到这些中心节点(引入社区异常)
- 属性,disproportionate(不成比例的):节点属性出现异常的值(过大或过小)。随机放大或缩小某些节点的属性的数值即可模拟
这些先验知识都是来自于某些现实的情况,比如垃圾邮件发送者会给大量的用户发送邮件(度大),垃圾用户发布垃圾帖子,这些用户很少被回复或关注(度小),后面两个异常属性比较好理解。应用了这四种先验知识之后,称此时的 graph 为 augmented attributed network 增强属性网络,表示为 \mathcal{G}_{ano}。上述的 label 都是 1(异常样本),正常的 label=0
知识集成 module
两件事:
- 学习 node rep
- 在不同的 view 上对比学习?
学习 node rep
用一个孪生 GNN(本质上就是一个 GNN,所谓权重共享在实现的时候根本是虚的,本质上强调的是“同时”完成两个 encoding,即对一个输入做了 encoding 之后,不会对网络进行更新就对下一个输入做 encoding)对 \mathcal{G} 和 \mathcal{G}_{ano} 同时编码,本文用的是 GAT。
不同视图 view 的对比
其实指的就是 \mathcal{G} 和 \mathcal{G}_{ano} 的对比,什么视图都是花里胡哨的。
采用两种对比策略:
-
Siamese contrast,孪生对比
对比的是异常和正常的节点嵌入。\mathcal{G} 被 encode 为 \bf{Z},\mathcal{G}_{ano} 被 encode 到 \hat{\bf{Z}},节点分别记为 \bf{z_i} 和 \hat{\bf{z_i} }。loss 如下:\mathcal{L}^{\mathrm{sc}}=\frac{1}{n}\sum_{i=1}^{n}(\mathrm{I}_{y_{i}=0}\cdot d\left(\mathbf{z}_{i},\mathbf{\hat{z}}_{i}\right)+\mathrm{I}_{y_{i}=1}\cdot\max\left\{0,m-d\left(\mathbf{z}_{i},\hat{\mathbf{z}}_{i}\right)\right\})- \text{I} 是指示函数,\mathrm{I}_{y_i=0}: 指示函数,当 y_i = 0 时,值为 1,否则为 0;\mathrm{I}_{y_i=1}: 指示函数,当 y_i = 1 时,值为 1,否则为 0。
- \mathrm{I}_{y_i=0} \cdot d(\mathbf{z}_i, \mathbf{\hat{z}}_i) 相似对样本损失(正常 vs 正常的距离要小):这里的损失是两个特征向量之间的距离 d(\mathbf{z}_i, \mathbf{\hat{z}}_i)。目标是最小化这个距离,使得相似样本对尽可能接近。
- \mathrm{I}_{y_i=1} \cdot \max\{0, m - d(\mathbf{z}_i, \hat{\mathbf{z}}_i)\} 不相似样本对(正常 vs 异常的距离要大):对于不相似样本对,损失是 \max\{0, m - d(\mathbf{z}_i, \hat{\mathbf{z}}_i)\}。目标是最大化这个距离,使得不相似样本对的距离至少为 m。如果 d(\mathbf{z}_i, \hat{\mathbf{z}}_i) 已经大于或等于 m,则损失为 0。
- 以上 loss 不包含“异常 vs 异常”的情况。
-
Triplet contrast,三元组对比
考虑连通的节点对 (i, j),j 是异常节点,i 是正常节点。之所以称为三元组,是因为这里面涉及到节点 i 的正常视图的 rep,和节点 j 在正常和在异常视图的 rep,loss 定义如下:\begin{aligned}\mathcal{L}^{\mathrm{tc}}&=\sum_{\begin{array}{c}\forall\mathbf{A}_{ij}=1,\\y_i=0,\end{array}}\max\left\{0,m-\left(d\left(\mathbf{z}_i,\mathbf{\hat{z}}_j\right)-d\left(\mathbf{z}_i,\mathbf{z}_j\right)\right)\right\}\end{aligned}备注: 这里补充一点,因为节点 j 是被异常注入处理过的,所以在 \mathcal{G} 中,j 还是被视为正常的节点,但是在 \mathcal{G}_{ano} 中,它是异常的节点,所以 j 会拥有两个视图(正常 and 异常视图),而 i 不管在哪个 \mathcal{G} 中,它都是正常的节点,所以只认为它有一个正常视图
本质上来看,是将 i 选定为了锚样本,它只有正常视图这一个视图,所以只有一个 embedding,即 \bf{z},而节点 j 有正常和异常两个视图,对应的 embedding 分别是 \bf{z_j} 和 \hat{\bf{z_j} },这里希望正样本 \mathbf{z}_j 与锚样本 \mathbf{z}_i 的距离 d(\mathbf{z}_i, \mathbf{z}_j) 小于负样本 \mathbf{\hat{z}}_j 与锚样本 \mathbf{z}_i 的距离 d(\mathbf{z}_i, \mathbf{\hat{z}}_j),也就是:
d(\mathbf{z}_i, \mathbf{z}_j) + m \leq d(\mathbf{z}_i, \mathbf{\hat{z}}_j)
Anomaly Detection
解码器:由一个 GAT 组成,通过 Z 去做重构,总过程和 loss 如下:
这里包含两个重构:结构和属性,结构(邻接矩阵 A)的重构方式很常见,就是属性的点乘(or 矩阵乘法)再激活,属性 X 的重构是用 GAT 做的。注意这里都是用的正常视图。
可以看出他是用 F 范数做的约束。
最后的 loss 为:
\eta是weight
疑问:为什么是\mathcal{L}^{\mathrm{cl}}\in\left\{\mathcal{L}^{\mathrm{sc}},\mathcal{L}^{\mathrm{tc}}\right\},难道每次只取其中之一???那怎么训练?
解答:确实是只是用其中一种,因为后面实验作者提出了两个变体,就是分别用了孪生损失和三元组损失的
方法小结
- 所谓先验知识的运用,其实就是异常注入。
疑问:如果是天生具有人工标注的异常数据集,那应该怎么办?岂不是失去了运用先验知识这一步,导致了节点j 不存在于正常视图?如何进行对比? - 可以理解为,作者一共做了两种下游任务来帮助获得更好的 rep,一个是对比,一个是重构
实验
数据集
- Flickr 有600个ground truth(有ground truth的时候他怎么处理的??)
- Amazon
- Enron
实验结果
| Dataset | Amazon | Enron | Flickr | ||
|---|---|---|---|---|---|
| LOF | 0.510 | 0.581 | 0.661 | 0.522 | 0.511 |
| DOMINANT | 0.592 | 0.716 | 0.749 | 0.554 | 0.571 |
| AEGIS | 0.556 | 0.602 | 0.765 | 0.659 | 0.645 |
| AnomalyDAE | 0.610 | 0.552 | 0.694 | 0.741 | 0.688 |
| CONAD-S | 0.635 | 0.731 | 0.782 | 0.612 | 0.670 |
| CONAD-T | 0.620 | 0.731 | 0.759 | 0.863 | 0.742 |
还有关于:
- 数据增强(利用的先验知识类别,去掉属性/结构的先验知识)
- 对比(去掉正常和异常视图之间的对比)
- 去掉重构
的消融实验,结果不放了,肯定是全功能的方法最好,去掉任何一种先验知识都会导致方法性能的下降


评论区