【论文阅读笔记】GAD-NR: Graph Anomaly Detection via Neighborhood Reconstruction
Title: GAD-NR: Graph Anomaly Detection via Neighborhood Reconstruction
Source: WSDM 2024
背景
Graph Anomaly Detection: GAD
异常的分类
上下文异常 contextual anomaly:(属性异常)属性与其他节点很大不同的节点,如垃圾邮件发送者或虚假账户持有者
结构异常 structural anomaly:具有不同的连接模式,如恶意卖家通过密集连接交换虚假评论,或机器人转发
联合异常 joint-type anomaly(没搞明白,是不是就是上面两个加在一起):如向电子邮件网络中不同社区的用户发送大量钓鱼邮件的节点
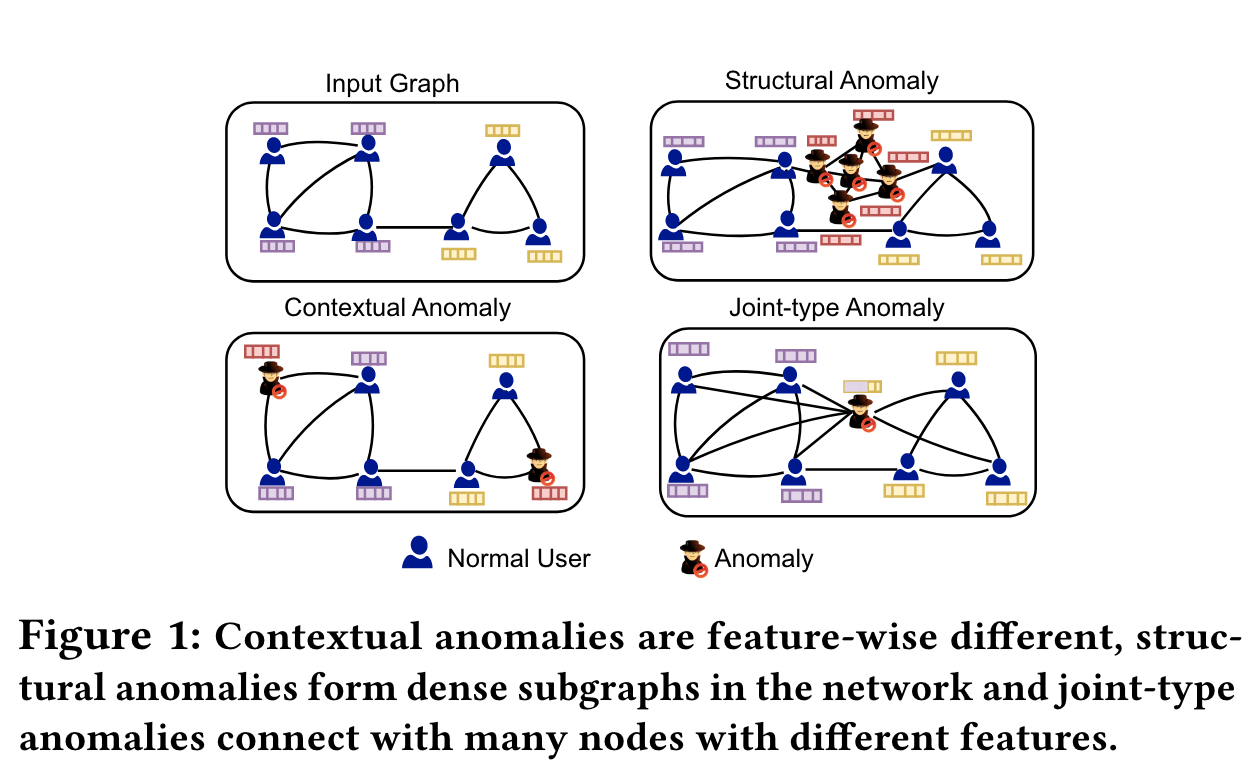
现有方法存在的问题:
- 只利用网络结构的方法:例如基于邻接矩阵的分解来检查中心性度量或聚类系数->只能检测结构异常
- 只利用节点特征的:比如最近邻->只能检测上下文异常
- GAE方法:基于节点表示重建边,这种约束能够让最初节点之间有边的节点在某个空间中分布的更近,对于检测本来就聚在一起的结构异常有效但不能检测没有聚在一起的异常。联合异常需要靠整个邻域才能检测出来
本文方法GAD-NR:
- 基于NWRGAE模型做的扩展,GAD-NR不是用proximity-driven loss来恢复边的,而是用降维了的节点表示来重建整个邻域。::这句话似乎是只对encoder部分说的,但是本文的重点在decoder啊喂!encoder没什么创新吧??::
方法
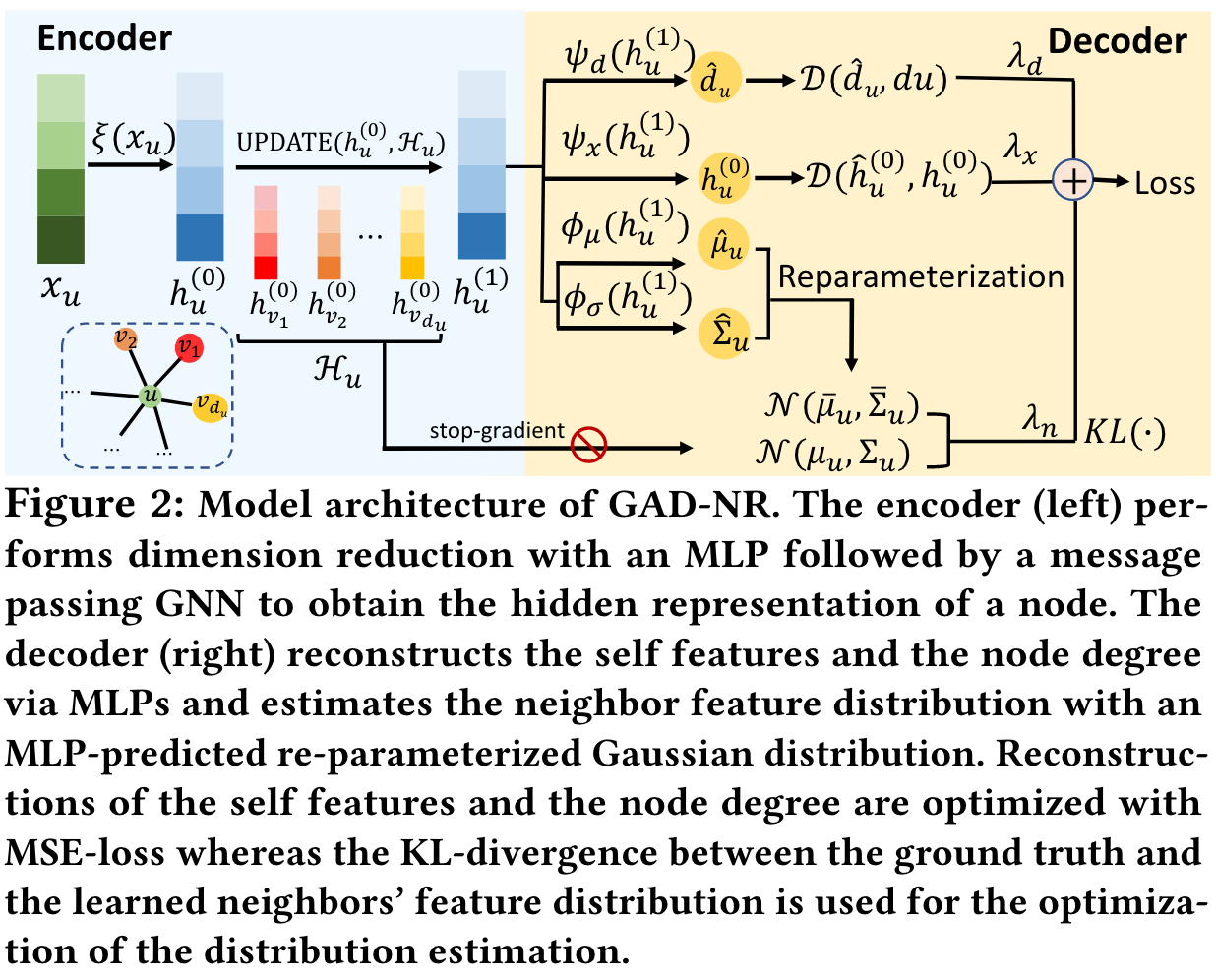
总体框架
-
encoder:左半边是encoder,x_u \rightarrow h_u^{(0)}是经过随机的线性映射得到的,因为x通常是极度稀疏的,h_u^{(0)} \rightarrow h_u^{(l)}是用GNN做的,将原始的节点表示变成representation,可以用GCN,Sage等等
-
自重构:通过MLP,\hat{h}_{\mathcal{u}}^{(0)}=\psi_{\mathcal{X}}(h_{\mathcal{u}}^{(1)}),重构损失是通过例如L2距离这样的距离函数实现的,这里产生一个loss:\mathcal{L}_u^x=\mathcal{D}\left(h_u^{(0)},\hat{h}_u^{(0)}\right)
-
邻居重构:对于每个节点,有两个东西需要计算:度和它的邻居的rep的分布信息
- 度:直接MLP+l2 loss \mathcal{L}_u^d=\mathcal{D}\left(d_u,\hat{d}_u\right)
- 根据h_u^{(L)}(和u的邻居)重构出邻居rep的分布\mathbb{P}_u(注意上标L是指第几层GNN的输出,文中默认只有1层):
细说邻居rep重构:(感觉作者没讲清楚,符号很混乱,以下是我的理解)
-
对于真实的给定\mathcal{H}_u=\{h_v^{(0)}|v\in\mathcal{N}_u\},通过以下方式估计这些feature满足的多元高斯分布的均值和协方差矩阵:
\mu_u=\frac1{d_u}\sum_{v\in\mathcal{N}_u}h_v^{(0)},\Sigma_u=\frac1{d_u-1}\sum_{v\in\mathcal{N}_u}(h_v^{(0)}-\hat{\mu}_u)(h_v^{(0)}-\hat{\mu}_u)^\top相当于把u的邻居的rep求平均当作均值。这里的均值和协方差矩阵后面会用来跟预测值对比求得一个优化目标。
疑问:为什么右边是减去\hat{\mu}_u,感觉是没道理的,因为hat的是预测的,跟真实的分布参数应该无关才对,怀疑是写错了?应该就是减去\mu_u
-
如何预测\hat{\mu}_u和\hat{\Sigma}_u?
\hat{\mu}_u=\phi_\mu(h_u^{(L)}),\quad\hat{\Sigma}_u=\mathrm{diag}(\exp(\phi_\sigma(h_u^{(L)})))备注:要求\phi_\sigma(h_u^{(L)})是非负的,再exp能保正,而exp(向量)就是逐元素exp,diag再构造对角阵,满足协方差矩阵的对称正定性。
-
基于\mathcal{N}(\hat{\mu}_u,\hat{\Sigma}_u),抽样(生成?)出q个符合这个分布的向量z_1到z_q,然后经过全连接层获得q个h,记为\bar{h}_1到\bar{h}_q。我自己简单测了一下这种方法的可复现性,这个从多元高斯分布进行随机采样过程代码实现可以这样:
# 生成多元高斯分布 # 使用 torch.distributions.MultivariateNormal mvn = torch.distributions.MultivariateNormal(mu, Sigma) # 设定采样个数 q q = 3 # 从分布中采样 q 个样本 samples = mvn.sample((q,))可视化出来的效果大致这样:
-
上面得到的h就称为重构的邻居特征 reconstructed neighnors' features,然后基于这些来计算它们的均值和协方差:
\bar{\mu}_u=\frac1q\sum_{i=1}^q\bar{h}_i, \bar{\Sigma}_u=\frac{1}{d_u-1}\sum_{i=1}^q(\bar{h}_i-\bar{\mu}_u)(\bar{h}_i-\bar{\mu}_u)^\top这个跟上面的式子是类似的。这里计算出的\bar{\mu}跟真实的\mu的区别在于前者比后者多了:MLP+抽样+FC。
-
通过KL散度衡量它们的误差:
\begin{equation} \mathcal{L}_u^n=\mathrm{KL}(\mathcal{N}(\mu_u,\Sigma_u)||\mathcal{N}(\bar{\mu}_u,\bar{\Sigma}_u))=\frac12[\log\frac{|\Sigma_u|}{|\bar{\Sigma}_u|}-p+\mathrm{tr}(\bar{\Sigma}_u^{-1}\Sigma_u)+(\mu_u-\bar{\mu}_u)^\top\bar{\Sigma}_u^{-1}(\mu_u-\bar{\mu}_u)] \end{equation}
最终的loss为:
几个\lambda都是超参数。
异常检测如何进行?——(没明说)看意思是根据Loss即可,越大的loss说明越难进行重构,说明更可能是个anomaly
几个注意点
存在一个假设
作者假设这一堆feature(h_u)满足多元高斯分布了,但是现实情况不一定会如此,猜测是经验上的依据,或者是依据中心极限定理(但是仍然不能保证每个h是独立同分布的,且n也不一定足够大),总之,这个假设虽然突兀但不是完全没有参考不了的东西的,所以我们假设这个假设是能接受的
为什么可以通过作者提到的公式来估计均值和协方差?
这是统计学中的常见估计方式
其他
GAD任务的模型的表达能力不应该太强,否则容易导致过拟合
为什么???表达能力强不应该就是更好吗??过拟合跟表达能力有什么必然联系吗?
实验(不详述,仅复述重要结论和原因)
实验设置
数据集:
- Cora
- Disney
- Books
- Enron

重要结论
-
关于几个\lambda的讨论


疑问:“结构+联合“异常是什么东西,这个概念是突然出现的,文中没有任何地方对他做了解释。也不明白这里的第二个表跟最上面的表有什么区别
现象:
- 普遍来看去掉neighbor reconstruction后,性能下降的最显著
- 去掉self-feature reconstruction后,上下文异常检测性能下降显著,结构+联合下降的不太明显
- 去掉degree reconstruction后,下降的都不是特别明显
- 现象是符合直觉、符合预期的
-
关于\lambda的超参数分析(两个数据集,三个\lambda)

疑问:每个图作者都说了是改变其中某一个\lambda,但并没有说其他不改的\lambda是如何取值的,而且他这里既然不是只有一个超参,而且重点应该不是数值本身,而是它在整个loss中的权重占比,所以是不是应该探究一个参数与另一个参数的比值,或者\lambda_1 / (\lambda_2 + \lambda_3)才更合理
疑问:如果我自己看这个图,我得出的结论就是,不管对何种类型的异常检测而言,我就调大\lambda,就能检测的更好,但是实际上你调大了一个\lambda,那么必定有另一部分的loss会变小,必然导致某一种类型的异常检测性能发生变化,也就是说这个图没意义。。。 -
关于rep维度的讨论:
Cora数据集上,从32提升到128时,性能有提升,Reddit从8到32也是提升,继续增大就会有负面影响,这组数据可以对我将来的实验起到一定超参选值的帮助
总体感受:文章有的重要观点都没有论证和引用,文中存在表述不一的地方,还有格式错误,就像是个半成品


评论区